Освещенность по вертикали

Все, что мы делали до этого, касалось только расчета затенения на плоскости, на которую падает тень. Это оправдано для цветов и невысоких кустиков. Кроны же у деревьев и высоких кустов могут подниматься над областью затенения и получать дополнительное освещение. Т.е. реально освещенность для деревьев будет гораздо больше, а затененность соответственно меньше. Попробуем подняться над плоскостью и учесть этот фактор.
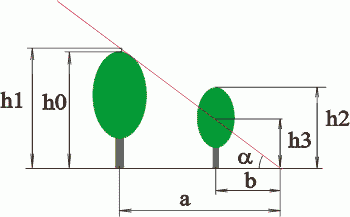
Для этого нам надо найти какая часть дерева будет находиться в тени, а какая на солнце, т.е. найти отношение h3/h2, назовем его x.
Здесь b' - это относительное расстояние рассчитываемого дерева от края тени. Т.е. берем от центра (первого дерева) до края тени радиус, на котором находится нужное нам дерево, и прикидываем, какая часть этого радиуса укладывается от дерева да края тени (напр. 0.5-посередине, 0.1- почти у края тени). Поскольку высота h1 (можно ее назвать эффективной высотой) немного отличается от истинной высоты дерева h0 и зависит от высоты солнца над горизонтом, для удобства сразу напишем на диаграмме ее значения для каждого сектора. В приводимом нами примере (а также см. приложения, где приведена полная диаграмма, напоминаем, что она построена для широты г. Брянска, т.е. подходит только для средней полосы) указаны высоты для 10-метрового дерева. Для других высот надо пересчитывать это значение, напр. для 20-метрового нужно брать 2h1 и т.д.
Когда мы нашли значение x, то можно оценить среднее значение освещенности (затененности) для дерева.
Уточненная затененность равна z'=x·z при условии, что x<1. Если x>1, то это значит, что крона дерева не поднимается над тенью. При учете суммарного затенения от нескольких деревьев: z'=x1·z1+x2·z2+...
Рассмотрим пример.

Пусть зеленым кружочком обозначено положение дерева высотой h2=2м. Его примерное положение b'=0.3. Тогда
Дерево такой высоты не поднимается над тенью.
Если h2=4м, то
z'=0.81·0.18=0.15
Чем выше дерево, или чем ближе оно сдвинуто к краю тени, тем больше уточненное значение затененности z' будет отличаться от плоскостной z.
Вроде простая математика, обычные пропорции, да не хочется на это отвлекаться. С самого начала мы задавались целью максимально упростить задачу и, по возможности, избежать рутинных расчетов. Поэтому нужно сделать еще один шаблон, "вертикальный", в котором будет учитываться изменение затененности по высоте. Для этого в каждой клеточке будем писать не затененность, а уже посчитанное значение b'·h1 из формулы:
С помощью нового шаблона (см. приложения) можно будет рассчитать (да, к сожалению, с калькулятором мы полностью не расстанемся) затененность для дерева любой высоты. Для этого значение из клеточки, соответствующей месту дерева, надо будет поделить на высоту затеняемого дерева. Но при этом надо будет контролировать с помощью первого шаблона, чтобы рассчитанная "вертикальная" затененность не превышала плоскостную для этого же места. Т.е. Порядок такой: рассчитываем z' - значение из клеточки делим на высоту дерева h2. Потом смотрим z в первом шаблоне в той же клеточке (как обычно). Если z'>z, значит, дерево полностью в тени, тогда для расчета берем z. Если z'<z, значит, дерево поднимается над тенью, тогда для расчета берем z'.
Итак мы получили два вида шаблонов, с помощью которых можно оценить затененность как для объектов, находящихся на плоскости, так и для объектов, поднимающихся над зоной тени. В приложении приведены как первый, более простой вариант диаграммы, который использовался для объяснения методики, так и ее усовершенствованный вариант. В усовершенствованном варианте затеняемая область расчерчена на клеточки с меньшей дискретностью, что позволяет делать расчет точнее. Для этого, в частности, проведены окружности через каждый метр (в рекомендуемом масштабе это 5мм), что позволяет точнее ориентироваться в расстоянии до дерева. В рассматриваемых далее примерах будут использоваться именно шаблоны усовершенствованного варианта.