Пример учета затененности деревьев

Имеется ряд светолюбивых деревьев высотой 6 м на расстоянии 5 метров друг от друга (три зеленых кружочка с номерами 1, 2, 3). На расстоянии 7 метров от центрального дерева растет дерево высотой 15 метров (голубой кружочек А).
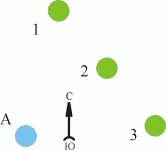
Дерево А будет отбрасывать тень на деревья 1, 2, 3. Кроме того, дерево 2 будет какое-то время отбрасывать тень на дерево 1, а дерево 3 - на дерево 2. Попробуем учесть и это. Для работы с примером нам понадобится шаблон №1 и шаблон №2 (см. приложения). Воспользуемся вторым способом работы с шаблонами и методом вспомогательных построений.
Оценим затененность дерева 1. Перевернем картинку и совместим дерево 1 с центром шаблона №2. Нарисуем штриховой красной линией направления к деревьям 1 и А. Построим вспомогательные "образы" деревьев 1 и А. Воспользуемся формулами: r'21=5*10/6=8.3 м (5 м- расстояние до зеленого кружочка 2, 6 м - высота дерева 2, 8.3 м - найденное расстояние до "образа" дерева 2) и r'А1=8.7*10/15=5.8 м Высота дерева 1, необходимая для оценки затененности (на эту величину делится значение из клеточки), тоже будет отличаться для каждой пары 2-1 и А-1. Чтобы ее найти, нужно умножить реальную высоту дерева 1 на тот же коэффициент, что и расстояние. Картинка просто пропорционально изменяется для каждого случая. h'1(2)=6*10/6=10 м (все правильно - высоты деревьев 1 и 2 совпадают, а, считая эти пропорции, мы как раз приводили высоту дерева 2 к "шаблонным" 10 м). h'1(А)=6*10/15=4 м
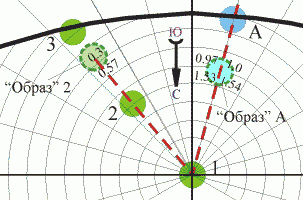
Из клеточек, на которые попадают "образы"-кружочки возьмем цифры (чтобы разгрузить рисунок, оставлены только эти цифры) для оценки освещенности. Затененность дерева 1 деревом 2 равна z'(2)=0.35/10=0.04 (0.35 - кружочек смещен книзу клеточки, аппроксимируем между 0.3 и 0.57, делим на 10 м - это h'1(2) (см. выше), пропорционально измененная высота дерева 1). Затененность дерева 1 деревом А равна z'(А)=1.3/4=0.33 (1.3 - аппроксимируем значения четырех клеточек, делим на 4 м - h'1(А)). Прежде, чем посчитать результирующую затененность, нужно сделать проверку с помощью шаблона №1, не превышают ли полученные величины соответствующие значения затененности на плоскости. Если это так (а наш метод не защищен от такого казуса), то нужно выбрать значение для плоскости. Т.е. из двух величин всегда выбираем наименьшую.

z(2)=0.16>0.04. Следовательно, выбираем значение 0.04. z(А)=0.32<0.33 - примерно одинаково, значит, дерево где-то на границе "выхода" из тени.
Вычислим результирующую затененность для дерева 1:
z1=z(2)+z(A)=0.04+0.32=0.36>0.14
Т.е. многовато. Теперь проведем такую же оценку для дерева 2. Совместим шаблон №2 с центром кружочка 2. Нарисуем "образы" деревьев 3 и А. Расстояние от центра шаблона до "образа" дерева 2 - r'32=5*10/6=8.3 м, пересчитанная высота для дерева 2 - h'2(3)=6*10/6=10 м. Расстояние от центра шаблона до "образа" дерева А - r'А2=7.2*10/15=4.8 м, пересчитанная высота для дерева 2 - h'2(А)=6*10/15=4 м.

Затененность дерева 2 деревом 3 равна z'(3)=0.35/10=0.04
Затененность дерева 2 деревом А равна z'(А)=1.31/4=0.33. Цифры совпали с предыдущими расчетами для дерева 1. Для дерева 3 это не удивительно - оно на таком же расстоянии от дерева 2, как дерево 2 от дерева 1. А вот для дерева А это действительно интересное совпадение - ведь расстояния и углы были разным�и. Теперь сделаем проверку шаблоном №1.

z(3)=0.16>0.04. Следовательно, выбираем значение 0.04. z(А)=0.2<0.33 - А здесь значения отличаются значительно, значит, дерево 2 погружено глубоко в тень от дерева А. Выбираем 0.2. Теперь вычислим результирующую затененность для дерева 2:
z2=z(3)+z(A)=0.04+0.2=0.24>0.14
Тоже многовато.
И наконец, оценим ситуацию для дерева 3. На него будет отбрасывать тень только дерево А. Совместим шаблон №2 с деревом 3. Нарисуем "образ" дерева А. Расстояние от центра шаблона до "образа" дерева А - r'А3=8.8*10/15=5.9 м, пересчитанная высота для дерева 3 - h'3(А)=6*10/15=4 м.

Затененность дерева 3 деревом А равна z'(А)=0.5/4=0.13
Делаем проверку шаблоном №1.

z(А)=0.07<0.13. Следовательно, выбираем значение 0.07. Результирующее значение будет таким же.
z3=z(A)=0.07<0.14
Дерево 3 оказалось в лучшем положении по сравнению с другими деревьями из ряда "зеленых кружочков".
Следующим нашим шагом найдем подходящее положение дерева А, чтобы оно не затеняло так сильно деревья 1 и 2, ведь вклад дерева А, как мы видим, наибольший. Попробуем "отодвинуть" дерево А в направлении, перпендикулярном ряду маленьких деревьев, хотя вообще-то можно двигать, куда угодно. Возьмем картинку, которую мы использовали при оценке затенения дерева 2, и нарисуем на нем "образ" дерева А в подходящем месте. Влияние других деревьев мы уже учли, и они сдвигаться не будут. Рассчитаем, какой вклад дерева А будет допустимым для дерева 2.
z2=z(3)+z(A)=0.14
z(A)=z2-z(3)=0.14-0.04=0.1
Затененность, которую будет давать дерево А, должна быть z(A)=0.1. При этом значение на шаблоне в клеточке должно быть x=z(A)*h'2=0.1*4=0.4.

Исходя из найденного положения "образа" для дерева А, пересчитаем положение самого дерева А. rА2=r'А2*15/10=8.3*1.5=12.5 м - расстояние от дерева А до дерева 2. Теперь проверим, достаточно ли это смещение для дерева 1, как мы это обычно делали. r'А1=12.5*10/15=8.3 м

z'(А)=0.4/4=0.1 (0.4 - среднее между 0.51 и 0.3)
z1=z(2)+z(A)=0.04+0.1=0.14
И здесь попали. С чем вас и поздравляю! Проверку шаблоном №1 можете выполнить сами, там все в порядке.
