Сад

Каждый творец своего поместья, конечно же, найдет свои варианты-изюминки и сделает из своего поместья шедевр искусства, соответствующий камертону его сердца. Естественно, практически невозможно рассмотреть все варианты, до которых смогут подняться люди-творцы в полете своей фантазии и вдохновения. Мы попробуем рассмотреть только простейший вариант регулярной структуры сада. Высота всех деревьев берется одинаковой и "удобной" для шаблона - 10 метров. Для регулярной структуры пересчитать расстояния для других высот деревьев будет очень легко - через пропорцию.
На первом рисунке изображен для начала всего лишь один ряд деревьев. Зеленые кружочки символически изображают деревья. Ряд расположен с севера на юг и поэтому каждое дерево затеняется другим деревом, растущим южнее, и, в свою очередь, отбрасывает тень на дерево, растущее к северу. "Теневая" картина показана на следующем рисунке.
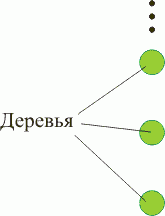

Для такой структуры достаточно рассмотреть всего лишь пару деревьев, чтобы узнать, на каком расстоянии нужно высаживать деревья в ряду, чтобы освещенность была приемлемой. Предположим, что деревья растут на расстоянии 4 метра. В нашем масштабе - это 2 см.

Здесь мы будем использовать первый (т.е. обычный) способ работы с шаблонами (о другом способе см. пример 1 и пример 2). Совмещаем центр "вертикального" шаблона (шаблона №2) с нижним деревом-кружочком, отбрасывающим тень на верхнее. Затененность для верхнего дерева получается как среднее между 2.1 и 2.77 деленное на 10 (высоту дерева) :
Получаем 0.24. Это многовато для садовых деревьев. Нужно меньше или равно 0.14. Постепенно увеличиваем расстояние, чтобы найти оптимальное. Оптимальным получается расстояние более 5.5 метров (в нашем масштабе - 2.75 см).

Затененность равна :
Итак, для однорядной структуры оптимальное расстояние с небольшим допущением 5.5 метров (ведь нам нужно 0.14, но для широты Брянска вполне пойдет и 0.15). Теперь усложним картину и рассмотрим влияние еще одного, добавочного ряда. На следующем рисунке стрелками показано, какие деревья и в каком направлении затеняют рассматриваемое дерево А.
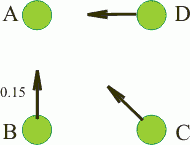
Вклад дерева B нам уже известен - 0.15 (пометим это на рисунке). Определим вклад дерева С. Для этого совместим центр шаблона с кружочком С и посмотрим, на какие цифры попал кружочек А. Получается середина между 0.39 и 0.57, 0.3 и 0.59. Да, приходится немножко аппроксимировать и усреднять. Если кружочек смещен в сторону другой клетки, то можно пытаться учесть и это. В общем, творческий подход. Таким образом, z'(C)=0.46/10=0.046

Теперь аналогично определим вклад дерева D. z'(D)=0.45/10=0.045
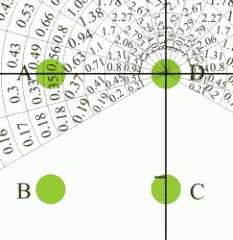
В результате получаем

z'сумм=0.15+0.046+0.045=0.24
Аналогичный расчет для расстояния 6 м дает z'=0.2
А для 7м:
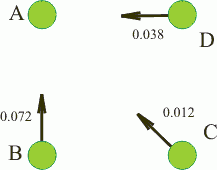
z'сумм=0.072+0.012+0.038=0.12
Т.е. расстояние 7 метров (и даже чуть меньше) является подходящим для двухрядной структуры.
Если добавить еще один ряд слева и рассмотреть трехрядную структуру (а она только немного меньше затененности для регулярной многорядной структуры сада, т.е. когда дерево находится внутри массива сада), то получим такую картинку (для 7 метров):

z'сумм=0.072+2*0.012+2*0.038=0.17
Опять затененность чуть-чуть превышает норму. Значит истина где-то между 7 и 8 метрами.
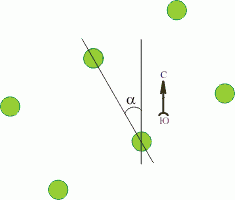
Это мы рассмотрели регулярную структуру, которая ориентирована строго по сторонам света, т.е. ряды идут с севера на юг и с запада на восток. Если структуру чуть-чуть повернуть относительно сторон света, то тени тоже повернутся и затененность изменится.
В следующей таблице приведены данные расчета затененности z' для различных структур при разных углах.

Заодно покажем, что из рассматриваемой структуры с высотой деревьев 10 метров, на которую "настроен" шаблон, можно получить цифры расстояний для структ�ур с другими высотами деревьев. Для этого надо полученное расстояние разделить на 10 ("удобная." для шаблона высота дерева в метрах) и умножить на нужную высоту. Для примера перепишем нашу табличку для высоты деревьев 6 метров.

Из таблицы видно, что более "экономичным" по расстоянию является квадрат, ориентированный с севера на юг (угол 0°). И все-таки мне больше нравится, хотя он выглядит самым неоптимальным, вариант, который я для себя назвал "соты". Что под этим имеется в виду - это деревья, расположенные по шестиугольникам.

Почему такая структура? Ну во-первых, надо заниматься не только расчетами. Все эти выкладки да шаблоны - это просто инструмент, который может помочь не допустить грубых ошибок. А вот в творчестве важнее слушать свои чувства. Т.е. мне такая структура просто нравится. Кроме того, такая структура ближе к природным и позволяет лучше использовать принцип биоразнообразия, который должен быть основополагающим. Принцип биоразнообразия - это когда растения имеют по соседству рядом с собой растения других, "неродственных" им видов, даже лучше дикорастущих. Это позволяет избежать монокультуры (односортности) в посадках, которая ведет к увеличению болезней и вредителей. Можно предложить, например, такую структуру (разные породы показаны разным цветом):

Видно, что из нашей структуры вырисовывается что-то похожее на узор, а это уже бесконечное поле для творчества.
