Пример учета затененности на плоскости

В качестве примера рассмотрим следующую простенькую задачу. Имеется три дерева высотой 10 метров, расположенных уголком, на расстоянии друг от друга 4 метра (на р�исунке три зеленых кружочка). Между ними можно поставить лавочку, а перед лавочкой пусть будет клумба (розовый кружочек).

С лавочкой, наверное все будет в порядке, а вот клумбе надо дать достаточно солнечного света. Конечно, это только пример. Он может показаться надуманным и искусственным. Одним клумбы вообще не нужны, все-таки "цивилизованный" элемент. Другие могут сказать, что по мере роста деревьев будут отодвигать клумбу, только и всего. Может быть и так. Хорошо, если будет, куда отодвигать. А так в направлении, куда надо двигать, может быть запланировано что-то другое, тогда придется вообще менять замысел.
Итак - пример, в котором нам потребуется шаблон №1 (см. приложения).
Для этого нарисуем все в "удобном" для шаблона масштабе - в 5 мм - 1 метр. Чтобы определить затененность в районе клумбы, нужно на каждое дерево положить шаблон и посмотреть, какое значение выпадает на клумбу. Потом полученные значения от всех трех деревьев нужно сложить. Результатом будет значение суточной затененности клумбы.

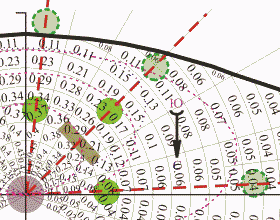
На рисунке показано совмещение шаблона с первым деревом. (Шаблон показан в виде фрагмента, для уменьшения объема) Мы видим, что на клумбу приходится значение между 0.17 и 0.26 . Притом видно, что чуть-чуть больше, чем среднее значение (будем проводить расчет на середину клумбы, хотя, возможно, было бы более правильно рассматривать самый затененный край, ближайший к группе деревьев). Учитывая все это принимаем, что вклад в суточную затененность от первого дерева будет - z1≈0.22.

Значение затененности от второго дерева находится между 0.37 и 0.4 - z2≈0.38
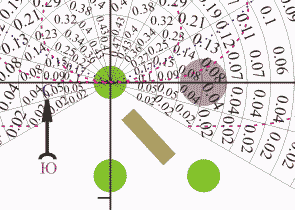
Значение затененности от третьего дерева находится между 0.04 и 0.08 - z3=0.06
Суммируя значения затененности от всех трех деревьев, получаем результирующую затененность для клумбы -
z=z1+z2+z3=0.22+0.38+0.06=0.66
Это значительно больше требуемых 0.14. Нам пока это не важно - мы учимся определять затененность.
Рассмотрим еще один метод нахождения суммарной затененности. Для этого нужно перевернуть шаблон и совместить его с серединой клумбы (т.е. с расчетной точкой), а значения затененности считывать с зеленых кружочков деревьев. Для удобства иллюстрации вместо переворачивания шаблона перевернем нашу картинку-план.

Мы видим, что зеленые кружочки попали в те же самые места, и им соответствуют значения затененности, которые мы обозначили как z1, z2, z3. И, естественно, их сумма даст то же самое значение для суммарной затененности - z=0.66. Первый способ более понятен с точки зрения физического смысла шаблона, поскольку шаблон - это область, на которую падает тень, а тень должна быть к северу от объекта, ее отбрасывающего. Зато второй метод, определенно оперативнее первого.
Теперь попробуем, постепенно увеличивая расстояние от клумбы до деревьев, скорректировать план, чтобы получить нормальную затененность.
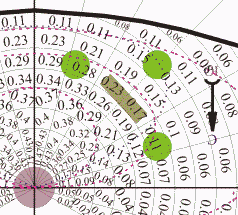
z=0.28+0.14+0.1=0.52 - многовато

А здесь видно, что центральное дерево уже вышло из зоны влияния, т.е. его тень не попадет на клумбу. Два других дерева дадут почти приемлемый вклад. z1=0.6÷0.8, z2=0.08, т.е. суммарное z≈0.14÷0.15. Но при этом клумба находится на расстоянии 12 метров от центрального дерева и 9.5 метров от боковых (расстояние легко считать по концентрическим окружностям, располагающимся через 1 метр). В общем, далековато от лавочки. Значит надо, что-то менять - либо расположение деревьев, либо ориентацию по сторонам света, либо высоту деревьев.
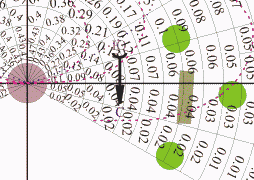
Например, таким поворотом при той же высоте деревьев мы смогли чуть-чуть сократить расстояние до клумбы. До центрального дерева - 10.5 м, до боковых деревьев и до лавочки - 8 м. Но лавочка стала более открытой для солнца.
Попробуем уменьшить планируемую высоту деревьев. Но для этого нам либо нужен другой шаблон (наш-то годится только для фиксированной высоты - 10 метров), либо надо научиться пользоваться нашим шаблоном для разных высот. Можно использовать десятиметровый шаблон, если пропорционально поменять масштаб плана. Например, для дерева высотой 5 метров (в два раза ниже 10 метров) нужно использовать масштаб в 1 см - 1 метр, т.е. увеличенный в два раза против нашего. И так далее. В общем-то нормальный подход, если используются деревья одной высоты. При наличии разных высот придется рисовать одну и ту же картинку в разных масштабах - это довольно сложно и муторно.
Можно все делать в одном масштабе (лучше нашем любимом - в 5 мм - 1 метр), но для этого нужно использовать вспомогательные построения. Что мы и будем делать.
Если дерево выше 10 метров, то для него требуется увеличение шаблона - площадь, "захватываемая" тенью, увеличивается. Области с определенной затененностью лежат на большем расстоянии от дерева. Чтобы не увеличивать шаблон, нужно поменять масштаб, а можно просто сделать "вид", что дерево стало высотой 10 метров, и поместить его в такую точку, чтобы оно создавало такое же затенение, как и дерево исходной высоты. Вот для этого и понадобятся вспомогательные построения. На следующем рисунке рассмотрим, как это делать для второго (оперативного) способа работы с шаблонами.
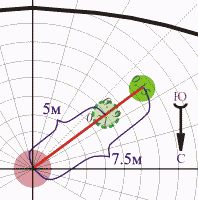
Красным отрезком показано направление между клумбой (розовый кружочек) и деревом высотой 15 метров, обозначенным зеленым кружочком. Естественно, такое высокое дерево даст затененность больше, чем указано в соответствующей клеточке шаблона (0.15). Цифры на шаблоне возрастают при приближении к центру, поэтому, чтобы затененность была большей, надо придвинуться к центру шаблона. Т.е. нам нужно найти как бы "гипотетический образ" десятиметрового дере�ва на шаблоне - клеточку, лежащую на той же красной прямой, но с затененностью, соответствующей нашему реальному дереву. Для этого вычисляем пропорцию:
, где r - расстояние от центра шаблона до высокого дерева, r' - искомое расстояние от центра шаблона до "образа" дерева на нашем шаблоне, h - высота дерева
Для нашего случая r'=7.5*10/15=5 м . На рисунке "образ" нарисован более светлым кружочком с штриховым контуром. Из клеточек под этим "образом"-кружочком считываем реальную затененность - z≈0.2. Еще раз повторяем, что "гипотетический" кружочек нужен только для оценки затененности деревьев с высотой, отличающейся от "шаблонных" десяти метров, реальное дерево "осталось" на месте темного зеленого кружочка.
Теперь рассмотрим пример, в котором на том же месте запланировано дерево с высотой не 15 метров, а 7. По нашей формуле r'=7.5*10/7=10.7 м. Т.е. вместо 0.15 такому дереву будет соответствовать затененность 0.08.

Теперь можно переходить к нашему примеру с лавочкой. Попробуем идти от обратного и найдем, какой высоты должны быть деревья, чтобы затененность клумбы была около 0.14, и чтобы от лавочки до клумбы было не более 4 метров.
Вначале нарисуем "образы"-кружочки, так чтобы суммарная затененность удовлетворяла условию "меньше или равно 0.14". Эти гипотетические "образы" должны лежать на прямых,, соединяющих центр шаблона (клумбу) и кружочки-деревья, чтобы не потерять направления. Центральное дерево нарисуем на уровне z=0.1, второе (верхнее на рисунке) дерево вынесем за пределы влияния, т.е. z=0, а третьему дереву достанется z=0.4. В сумме z=0.14, как положено. Измерив расстояния от кружочков до центра шаблона, можно через формулу посчитать, какие высоты деревьев будут соответствовать выбранным "образам".
h1 =10*r1 /r'1 =10*6.5/10=6.5 м
h2 =10*r2 /r'2 =10*4.7/9.3=5.1 м
h3 =10*r3 /r'3 =10*4.4/12.5=3.5 м
Теперь, исходя из полученных цифр высот, мы можем подобрать подходящие породы деревьев или кустов. Или опять попытаться оптимизировать расположение деревьев или их высоты. Мы этому уже научились.
